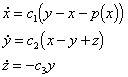
The dynamical system
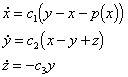
where
represents a mathematical model of
an LRC circuit consisting of a linear resistance, two linear capacitances,
a linear inductance and a non-linear diode. The parameters of the system
satisfy 
, 
.
There are three equilibrium points
The characteristic polynomial for the equilibrium point at the origin is
Thus 
and
hence the equilibrium point is unstable.
The characeristic polynomials for the two equilibria are identical and given by
There is a bifurcation at
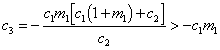
where the equilibrium point changes
from unstable to stable as 
becomes
greater than the bifurcation value.
SIMULATION
Taking parameter values 
the
critical value of 
.
The plots below show the behaviour of the system as is
decreased.
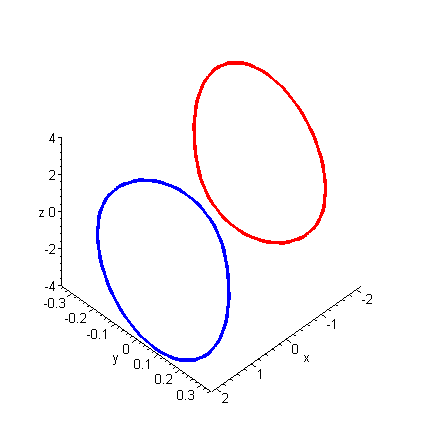
Pair of Limit Cycles
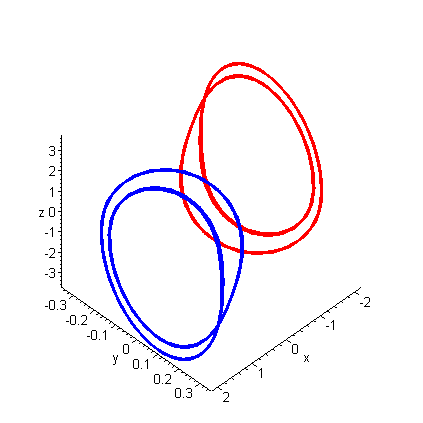
Period Doubling
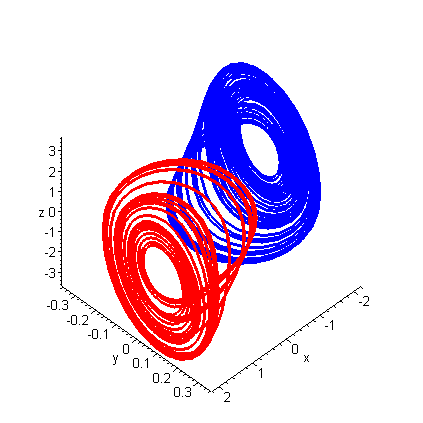
Two Strange Attractors
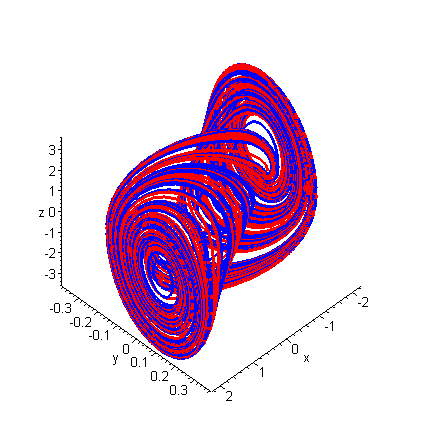
The Double Scroll Attractor
The link below provides a Java simulation of the system.
Parameter values and initial conditions can be changed.
An alternative series of simulations is available using Maple.