A powerful method introduced by
Poincaré for examining the motion of dynamical systems is that
of a Poincaré section. Let S be an n-1 dimensional
surface transverse to the trajectories of a dynamical system. Consider
a point ![]() on S at time
on S at time ![]() .
As the trajectory starting at
.
As the trajectory starting at ![]() evolves it will eventually return to S at
evolves it will eventually return to S at ![]() after a certain period . If we consider all initial points on S
we can define a mapping P from S to itself such that
after a certain period . If we consider all initial points on S
we can define a mapping P from S to itself such that
![]()
and in general after ![]() intersections
intersections
![]()
The mapping P is called the return map or Poincaré map of the dynamical system.
We can use this method to investigate the behaviour of the non-autonomous system, considered previously,
in the following way. Choose a Poincaré section consisting of the
x-y
plane. Choose a strobe frequency![]() which
is hopefully the period of a potential periodic attractor. Only plot points
in the x-y plane corresponding to a time interval
which
is hopefully the period of a potential periodic attractor. Only plot points
in the x-y plane corresponding to a time interval ![]() .
Then on ignoring transients:
.
Then on ignoring transients:
For a periodic attractor and the correct strobe frequency we will only observe one plotted point in the x-y plane.
If the natural frequency of the system is ![]() and
and ![]() then
we will obtain q points. If the natural frequency is an irrational
multiple of the strobe frequency we will obtain a closed curve on the Poincaré
section.
then
we will obtain q points. If the natural frequency is an irrational
multiple of the strobe frequency we will obtain a closed curve on the Poincaré
section.
If we do not in fact have a periodic attractor but a chaotic attractor
the Poincaré section will be fractal in nature.
Below are some Poincaré sections for different values of the parameter B in the system considered above with strobe frequency equal to the forcing frequency.
![]()

Recall that the plot of trajecories showed periodic behaviour.
![]()
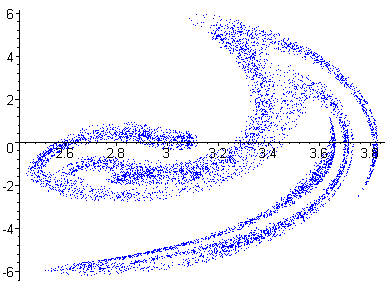
In this case the plot of trajectories suggested that there was a strange
attractor. The Poincaré section shows a fractal attractor known
as the Ueda Attractor.