be the state of the dynamical system. The function 
tells us how the system moves, e.g.EQUILIBRIUM POINTS
Let the vector be the state of the dynamical system. The function tells us how the system moves, e.g.
In special circumstances, however, the system does not move. The system can be stuck (we shall say fixed) in a special state. We call these states fixed (equilibrium) points of the dynamical system.
Consider the system
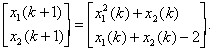
This may be rewritten as 
where
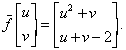
In order to find equilibrium points we solve the equations
from which one can find 
The equilibrium points can be stable, unstable or semistable. Suppose a first order dynamical system has an equilibrium value 
This equilibrium value is said to be stable or attracting if there is a number 
, unique to each system, such that, when
then 
An equilibrium value is unstable or repelling if there is a number 
such that, when
then
for some, but not necessarily all, values of 
Note that 
is a measure of the distance between the two values 
and 
The definition states that an equilibrium value is stable if whenever 
is sufficiently close to then 
tends to
The equilibrium point is called marginally stable or neutral provided the following: for all starting values near the system stays near but does not converge to .
Consider a dynamical system (called a general affine system)
Theorem: The equilibrium value 
for this dynamical system is stable, if 
for any value of 
Also, if 
then the equilibrium value is unstable and 
goes to infinity for any 
The equilibrium value is called semistable if for some values of 
tends to 
while for others goes away from 