Henon considered the pair of difference equations with

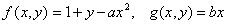
for given parameters 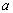and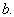

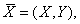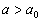There are two fixed points if where

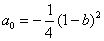
and

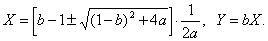
Henon and Pomeau interpreted the map geometrically as the product of successively a folding, a contraction (when 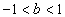) and a reflection in the line 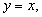and showed that the map is a canonical form to which any quadratic map with a constant Jacobian may be reduced by a linear transformation.

The composite transformation yields the Henon mapping.

1. The Henon map is invertible. This property is the counterpart of the fact that in the Lorenz system, there is a unique trajectory through each point in phase space. In this respect the Henon map is superior to the logistic map, its one-dimensional analog. The logistic map stretches and folds the unit interval, but it is not invertible since all points (except the maximum) come from two pre-images.
2. The Henon map is dissipative. It contracts areas, and does so at the same rate everywhere in phase space. This property is the analog of constant negative divergence in the Lorenz system.
3. For certain parameter values, the Henon map has a trapping region.
   In other words, there is a region 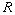that gets mapped inside itself.
4. Some trajectories of the Henon map escape to infinity.
   In contrast, all trajectories of the Lorenz system are bounded, they all eventually enter and stay inside a certain large ellipsoid.