It is often useful to be able to rule out the existence of a limit cycle in a region of the plane. The following result due to Dulac sometimes enables us to do this.

Dulac's Criterion

Let D be a simply connected region of the phase plane. If there exists a continuously differentiable function  such that

is of constant sign in D then the dynamical system

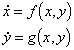
has no closed orbits wholly contained in D.

This method suffers from the same problem as finding Lyapunov functions in that it is often difficult to find a suitable function . Some possible choices for  are

• Worked Example 5

has no closed orbits anywhere.
 

Let us try .

Although this shows that there is no closed orbit contained in either half-plane  it does not rule out the existence of a closed orbit in the whole plane since there may be such an orbit which crosses the line .

Now let us try .

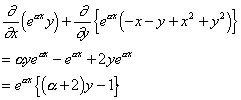
Choosing  reduces the expression to  which is negative everywhere. Hence there are no closed orbits.