1.4.1 The harmonic oscillator

A mass attached to the end of a spring and oscillating about the rest position is called a harmonic oscillator. It has many practical uses including suspensions on motorbikes and cars and pendulum clocks. Its motion can be represented by a second order differential equation of the form

where p and q are constants and and . For a derivation of this equation click here.
 

Representation as a pair of linear equations.

Substituting

the equation becomes

To find the equilibrium point

The equilibria occur when

There is only one equilibrium point at (0,0) provided that 

and q is a positive constant so 

Thus there is only one equilibrium point at (0,0).
 
 

To classify the equilibrium point

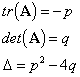
Consider p=0

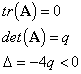
Looking at the tr-det diagram it can be seen that the equilibrium point is a neutrally stable centre. Practically this represents undamped motion as p is the damping constant. The solutions are periodic and oscillate forever with constant amplitude.

As an example consider p=0, q=4

Click on example to open the appropriate Maple window.

Consider 

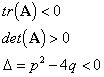
Using the tr-det diagram the equilibrium point is a stable spiral (focus).

Practically this represents damped motion with the solutions oscillating with decreasing amplitude as they tend to the rest position.

As an example consider p=2, q=4

Click on example to open the appropriate Maple window.

Consider 

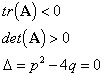
Using the tr-det diagram the equilibrium point is a stable degenerate node. It is not a star node since the matrix A is not diagonal. It is therefore an improper stable node.

Practically this represents a critically damped system. The trajectories no longer oscillate as they tend to the rest position. There is one directrix.

As an example consider p=4, q=4

Click on example to open the appropriate Maple window.

Consider 

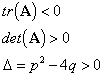
Using the tr-det diagram the equilibrium point is a stable node. The system is now over damped and again no oscillations take place. There are two directrices.

As an example consider p=5, q=4

Click on example to open the appropriate Maple window.