1

1.2 MATRIX ALGEBRA

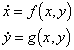
In this section you will learn some matrix algebra which will help you to understand the analysis of systems of differential equations. You will learn

To find equilibrium points

To find the trace and determinant of a matrix

To find eigenvalues and eigenvectors of a matrix

To find equations of directrices

To determine the type of eigenvalues

1.2.1 Equilibrium points

An autonomous pair of first order differential equations have the general form

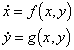
When a trajectory starts at an equilibrium point it remains there indefinitely. Thus, at an equilibrium point

Worked example 1

You are going to find the equilibrium points of the system given by

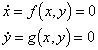
Click on example 1 to open the Maple worksheet.

1.2.2 Trace, determinant and discriminant of a matrix

Any pair of linear differential equations has a matrix associated with it. The linear system

can be written in matrix form

where

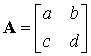
There are three quantities concerned with matrices which you will need to be able to evaluate. These are the trace, the determinant and the discriminant usually denoted by .

determinant(A)=det(A)=ad-bc

trace(A)=tr(A)=a+d

Worked example 2

You will find this in the handbook.

1.2.3 Equilibrium points of a linear system

For the linear system

at an equilibrium point

Summary

There is a single equilibrium point provided that

. In this case the system is said to be simple.

If the system needs further investigation. There could be additional solutions or no solutions and the system is said to be nonsimple.

worked example 3

You will find this in the handbook

1.2.4 Directrices or assymptotes.

These are straight line solutions. Thus any point starting on the trajectory remains on the trajectory for all time. They are found from the eigenvectors and the equilibrium point.

The eigenvaluesof a matrix

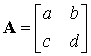
satisfy the characteristic equation which is given by

which is the same as

The eigenvectors X satisfy

If is a real eigenvector of A and the equilibrium value is then since the equilibrium point is not at the origin using a simple transformation the equation of the directrix is

where k can take any value.

Here is a worked example for you to study. Click on worked example 4 to open the Maple window.

Summary

It is only real values of the eigenvalues

which have practical importance . These correspond to real eigenvectors and real directrices.

If there are two real eigenvalues there will be two eigenvectors and two directrices.

If there is one repeated eigenvalue there are two possibilities. If the matrix is not diagonal there will be one eigenvalue and one directrix. If the matrix is diagonal there will be an infinite number of eigenvalues and an infinite number of directrices.

If the eigenvalues are complex there will be no directrces.

1.2.5.Types of eigenvalues

Since it is the nature of the eigenvalues which determines the number of directrices it is not always necessary to find their actual values.

Since the eigenvalues satisfy the quadratic equation

then will be real or imaginary depending on the sign of the discriminant given by

Investigation 1

You are going to investigate the eigenvalues when

>0, det(A)> 0 and tr(A) > 0
>0, det(A)> 0 and tr(A) < 0
>0, det(A)< 0

Click on investigation 1 to open the Maple window. When you have finished the investigation fill in the appropriate sections in the table in the handbook.

Investigation 2

You are going to investigate the eigenvalues when

<0, tr(A) > 0
<0, tr(A) < 0
<0, tr(A) = 0

Click on investigation 2 to open the Maple window. When you have finished the investigation fill in the appropriate sections in the table in the handbook.

Investigation 3

=0, tr(A) > 0
=0, tr(A) < 0

Click on investigation 3 to open the Maple window. When you have finished the investigation fill in the appropriate sections in the table in the handbook.

From these investigations it is clear that the nature of the eigenvalues can be determined from the three quantities trace, determinant and discriminant.

Worked example 5

You will find this in the handbook