In this section you will learn to
1.1.1 Systems of differential equations
This course is about predicting the long term behaviour of systems which can be modelled by differential equations. There are many different types of differential equations but in this section we will only study autonomous systems of first order equations.
A pair of autonomous first order differential equations have the general form
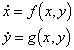
If the system is linear then the functions 
are linear and the system is of the form
Any second order differential equation of the form
A description or the method and examples of converting a second order
differential equation into a pair
of first order differerential equations can be found in the handbook.
Consider the harmonic oscillator with damping given by the equations
Click on field plot to open the Maple work sheet
for producing the diagram.
1.1.3 Drawing the phase portrait
The next step is to turn this field diagram into a phase plane diagram
by drawing trajectories through a selection
of initial points scattered over the x-y plane.
Click on phase plot to open the Maple worksheet
for producing a phase plot
1.1.4 Interpreting the phase portrait
Look at the phase portrait below.
Suppose you start at the point A. As t increases x increases
and y decreases until x reaches a positive maximum at
. Then x
and y both decrease until y reaches a negative minimum. Finally
x
decreases
and y increases as the
point approaches 
.This
behaviour can be confirmed by looking at the time series plots of x and y
against t. Click on x-t plot
and y-t plot to open the maple
worksheets to show you how to do this.
Can you describe what happens if you start at the point B?
Can you find the equilibrium point?
Which way are the arrows pointing? Do you think the point 
is
stable or unstable?
Can you find the asymptote? In this diagram there is only one.
Write your answers in the space provided in the handbook.