The output of a discrete variable method is a set of points and the output of the dynamical system is a continuous trajectory . For the numerical results to provide a good approximation to the trajectory we require that the difference

where is some defined error tolerance, at each solution point. This difference is called the global error and is the accumulated error over all solution steps. Unfortunately it is extremely difficult to accomplish this and we have to confine ourselves to controlling the local error

at each step where is the numerical solution obtained on the assumption that the numerical solution at the previous solution point is exact.

There are two sources of local error, the roundoff error and the truncation error.

Roundoff Error

The roundoff error is the error which arises from the fact that numerical methods are implemented on digital computers which only calculate results to a fixed precision which is dependent on the computer system used. Note that since roundoff errors depend only on the number and type of arithmetic operations per step and is thus independent of the integration stepsize h.

Truncation Error

The truncation error of a numerical method results from the approximation of a continuous dynamical system by a discrete one. The truncation error is machine independent, depending only on the algorithm used and the stepsize h.

An important concept in the analysis of the truncation error is that of consistency. Basically consistency requires that the discrete variable method becomes an exact representation of the dynamical system as the stepsize . Consistency conditions can be derived for both Linear Multistep and Runge-Kutta methods.

Linear Multistep Methods

Consider the general linear multistep method

We can define the first characteristic poynomial by

and the second characteristic polynomial by

We can show that consistency requires that

Runge-Kutta Methods

The general pth order Runge-Kutta method can be written in the form

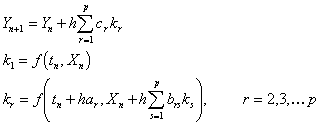
Here we have

and it can be shown that consistency requires that

• Worked Example 4

(a) the classical 4th order Runge-Kutta method,

(b) the two-step Adams-Bashforth method.

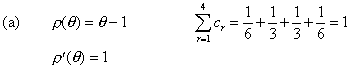
thus

and hence the method is consistent.

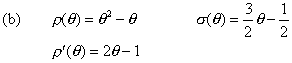
thus

and hence the method is consistent.

The accuracy with which a consistent numerical method represents a dynamical system is determined by the order of consistency. The method of determining this is best illustrated by an example.
 
 

• Worked Example 5

Maple Solution

The order of consistency is determined by substituting the exact solution into the formula of the numerical algorithm and expanding the difference between the two sides of the formual by Taylor series. The result is then normalised by multiplying by the scaling factor .

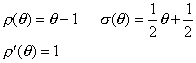
thus

and the method is consistent. Now the truncation error is given by

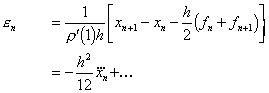
The order is given by the highest power of h remaining. Hence the method is consistent of order two.