![]()
Maple contains a large range of numerical procedures for integrating non-autonomous dynamical systems of the type
![]()
All of these procedures are invoked using the Maple dsolve command with the numeric option. The syntax for the command is
dsolve(deqns, vars, type=numeric, options)
where deqns defines the system of differential equations and initial
values, vars defines the dependent and independent variables, type=numeric
tells Maple to use a numerical algorithm and options allows a choice of
method, stepsize and other options associated with the method. The default
method is a Fehlberg fourth-fifth order Runge-Kutta method.
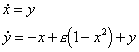
Classical Methods
Maple contains a number of one-step methods for the numerical solution
of initial value problems. These are referred to as classical methods and
are invoked by including the option method=classical[type] in the call
to dsolve. Here type can be one of
| foreuler | the forward Euler method; |
| heunform | the Heun formula (also known as the trapezoidal rule, or the improved Euler method); |
| impoly | the improved polygon method (also known as the modified Euler method); |
| rk2 | the second-order classical Runge-Kutta method; |
| rk3 | the third-order classical Runge-Kutta method; |
| rk4 | the fourth-order classical Runge-Kutta method; |
| adambash | the Adams-Bashford method (a "predictor" method); |
| abmoulton | the Adams-Bashford-Moulton method (a "predictor-corrector" method). |
If no type is specified the forward Euler method is used.
Worked Example 2 - The Forward Euler Method
Consider the IVP
![]()
Worked Example 3 - The Classical Second Order Runge-Kutta Method
Consider the solution of the IVP
![]()