Although the dynamical systems which we are simulating are usually in more than one dimension we can, without loss, restrict our numercal anlaysis of the methods to the single non-autonomous differential equation

subject to the initial condition . We shall usually refer to the differential equation together with the initial condition as an initial value problem (IVP). Discrete variable methods yield a series of approximations

on the set of points

where h is the stepsize.

Taylor Series Method

These methods are based on the Taylor series expansion

If the series is truncated and  is replaced by the approximation  we obtain the Taylor Series Method of order p

where .

Although there is an implementation of this method in Maple it is not much used in practice due to the necessity of computing the higher order derivatives of X. We shall only use it as a reference method when discussing the accuracy of other methods.

Runge-Kutta Methods

These methods are based on the notion of finding a formula which agrees with the Taylor series as closely as possible without involving derivatives. For example consider the possibility of matching the second order Taylor series method

by using a formula of the form

Two of the more popular methods are the improved Euler method

the modified Euler method

The procedure above can be extended to give higher order methods such as the classical 4th order method

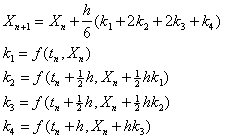
Linear Multistep Methods

These methods are based on integration of an interpolating polynomial having the values  on a set of points  at which  has already been computed. By integrating

over the interval  we obtain

Using various approximations ro the integral gives rise to the different methods. For example using linear interpolation we obtain the Trapezoidal method

The general form of these methods is

where  and  are constants, . This formula is called a linear k-step method. In order to generate the sequence of approximations  it is first necessary to obtain k starting values . If  the method is explicit. If  then the method is implicit and leads to a non-linear equation for .

The main methods of this type which we shall consider are:

Adams-Bashforth

These methods are explicit with methods of order k being k-step. Methods of order from one to three have the formulae

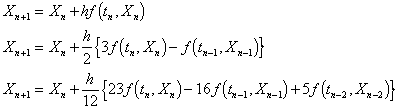
The first order method is more normally called the Euler method.

Adams-Moulton

These methods are implicit with methods of order k being -step. Methods of order from one to three have the formulae

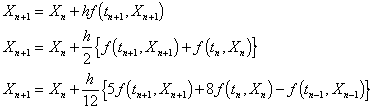
The first order method is called the backward Euler formula and the second order method is the Trapezoidal method.

Gear Methods

These methods are implicit with methods of order k being k-step. Methods of order from one to three have the formulae

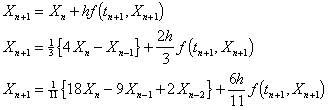
The first order method is again the backward Euler formula.