This is a problem peculiar to consistent linear k-step methods in which a first order dynamical system is integrated using a kth order difference equation. This leads to the possible existence of spurious solutions of the difference equation which can swamp the desired solution. In order to avoid this occuring we have to restrict the roots of the first characteristic polynomial  to satisfy the root condition.

Definition – Root Condition

We say that a linear k-step method satisfies the root condition if the roots of the characteristic polynomial  all lie within or on the unit circle, those on the unit circle being simple.

Note that the roots of  may be complex hence the necessity of considering the unit circle rather than the interval  in the definition.

Theorem – Zero-Stability

A a linear k-step method is zero stable if and only if it satisfies the root condition.

We can now state the fundamental theorem concerning convergence:

Theorem - Convergence

A discrete variable method is convergent if and only if it is both consistent and zero stable.

Often it is desirable for the roots of  to satisfy the strong root condition.

Definition – Strong Root Condition

A linear k-step method is said to satisfy the strong root condition if the characteristic polynomial has a simple root at  and all the remaining roots lie strictly within the unit circle.

The roots  of  for a consistent method satisfying the root condition can be categorized as

• Worked Example 6

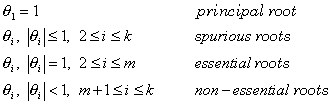
is convegent.

Before determining the characteristic polynomials write in the standard form

Then

Checking consistency

The roots of  are given by

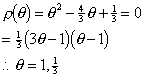
and hence the method is zero-stable.

Combining these results we can conclude that the method is convergent.