4.5.4 Comments and exercises

It is worthwhile to note that the fish population can develop in the condition that the harvesting rate h < Mc/4. If h > Mc/4 the species will disappear.

Exercises

1. Obtain the equilibrium populations which will apply to the logistic model. Investigate stability. Prove that the harvesting rate must be less than .
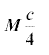2. Solve the logistic equation and verify the results of Exercise 1.
3. Derive the discrete time model of logistic growth.
4. Include harvesting in your discrete model.
5. For the continuous logistic model with harvesting, obtain a plot of the solution given that M = 50, c = 0.5, P₀ = 10, h = 5. Investigate the behaviour of the solution for a range of values of P₀ and a range of values of hh Comment on the behaviour of the solution from a mathematical point of view and from a modelling point of view.