A simplified economic model of a national economy with investment is represented by the dynamical system
where y is the national product and 
is
the investment function.
Stability Analysis
It is clear that the system has a single equilibrium point at the origin for all r. The Jacobian matrix is given by
and 
, 
and
hence the equilibrium point is an attractor if 
and
a repeller if 
where 
.
The eigenvalues of the Jacobian matrix are given by
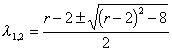
which are given by 
at 
.
Also
Thus all the conditions of the Hopf Bifurcation theorem are satisfied
except for the asymptotic stability of the origin at .
Asymptotic Stability of Origin
Introduce the Lyapunov function 
then
on the trajectories
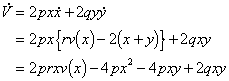
Now choose 
to
eliminate the cross term and
Thus at
But
hence we have the plot shown below.
Thus, if 
, 
and
if 
, 
and
thus 
with
inequalityonly on the line 
which
is not a trajectory of the system. Hence the origin is asymptotically stable
and there must be a supercritical Hopf bifurcation at .
Limit Cycle
The limit cycle is shown below for parameter value 
.
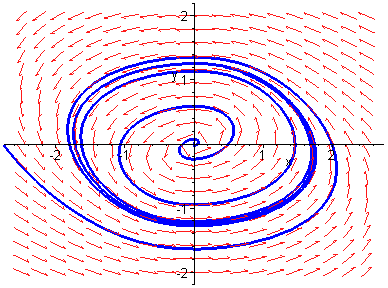
Unstable Focus + Stable Limit Cycle
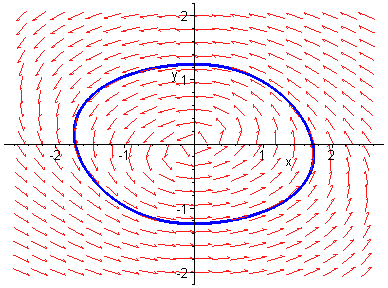
Limit Cycle