Download Handbook

Thus far in our study of dynamical systems the only type of attractors or repellers encountered have been point attractors or repellers i.e. stable nodes and foci or unstable nodes and foci. We shall now show that another type of attractor or repeller is possible for nonlinear systems, the limit cycle.

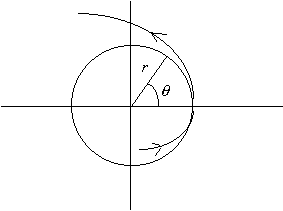
Polar Coordinates

Often it is advantageous to rewrite a dynamical system in polar coordinates when considering limit cycles. Recall the relationships between polar coordinates  and cartesian coordinates 

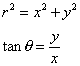
and the inverse relationships

Differentiating the former relationships with respect to t we obtain

and

At an equilibrium point we must have either  or .

Consider the system

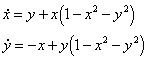
The polar form is

From these results two obvious solutions are  and .

The first solution corresponds to an unstable focus at the origin.

The second represents the polar form of the equation of a circle of radius one and centre the origin.

The fact that  implies that the circle is traversed in a clockwise direction with a constant angular velocity of one unit.

Thus we have a solution of the system which is a closed orbit.. Notice that if  then  and trajectories spiral outwards towards the closed orbit. If  then  and trajectories spiral inwards towards the closed orbit.

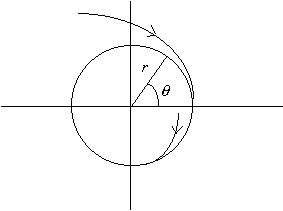
Overall the trajectories approach an isolated closed orbit which we call a stable limit cycle.

Other types of limit cycles are possible. For example

represents a system with an unstable limit cycle. In this case if  then  and trajectories spiral inwards away from the closed orbit. If  then  and trajectories spiral outwards away from the closed orbit.

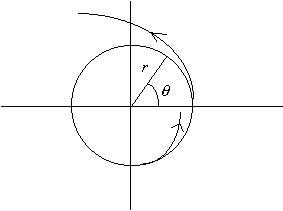
A third possibility is represented by the system

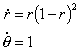
In this case we have a semi-stable limit cycle in which if  then  and trajectories spiral outwards towards the closed orbit. If  then again  and trajectories spiral outwards away from the closed orbit.