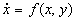
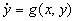
2.3 GLOBAL STABILITY
In this section you will investigate
The concept of a conservative dynamical system is important in real world applications. Conservative systems are ones in which a quantity is conserved in the sense that it is constant on any trajectory of the system. Often the conserved quantity has a physical meaning such as the total energy in the case of a system arising in classical mechanics or spin in the case of quantum mechanics. The following definition provides a formal statement of the concept.
If for the system
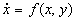
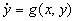
there exists a function E(x,y) such that its partial derivatives are continuous and E(x,y) satisfies the following conditions
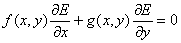
for all (x,y)
To verify a function is a conservative quantity for a system.
Here is a worked example to illustrate a method of verifying that a function is a conservative quantity
Finding Conserved Quantities using First Integrals
It is difficult to find a conserved quantity E(x,y), One method of doing this is to find a First Integral of the system. First integrals are conserved quantities provided they exist for all (x,y) in the plane.
In the problems that you will meet E(x,y) can be found by finding a First Integral. Here is a worked example to illustrate a method of finding a First Integral.
Finding conserved quantities using the total energy
In many dynamical systems the total energy is a conserved quantity. This method is explained and illustrated in worked example 3 in the module coursebook.
Phase portrait of a conservative system.
How can the existence of a conserved quantity for a nonlinear system help us to understand the long term behaviour of that system?
Investigation 1
You are going to compare the global phase portrait of a nonlinear system with the level curves of a conserved quantity for that system. Click on investigation 1 to open the Maple window which contains the material for this investigation
This investigation shows that if we can find a conserved quantity E(x,y) for a nonlinear system then the solution curves of the nonlinear system are the same as the level curves of the conserved quantity.
Stability of Equilibria in a Conservative System
If an equilibrium point also satisfies
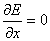
and
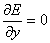
it is also a stationary point of E(x,y).
To classify the stationary point we need to look at the eigenvalues of the Hessian Matrix ;
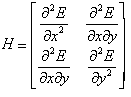
If the eigenvalues are
This gives a method of proving the existence of a nonlinear centre.
If the equilibrium point is a saddle for E(x,y) then the equilibrium point is unstable and a nonlinear saddle.
Determination of the existence of a nonlinear centre using a conservative system.
One of the limitations of the linearisation theorem is when the equilibrium
point of the linearisation is a centre. It does not follow that the equilibrium
point of the nonlinear system is also a centre and further investigation
is necessary. We can now do this further analysis for a conservative system.
The method is illustrated in the following example. Click on worked
example 4 to open the appropriate Maple window.
2.3.2 Reversible Systems.
Many dynamical systems have time-reversed symmetry in the sense that their behaviour is independent of the direction of time. For example a film of a swinging undamped pendulum would appear to be the same whether played forwards or backwards.
Definition: A plane dynamical system
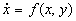
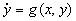
is said to be reversible if the equations are invariant under the change of variables
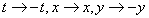
or
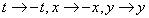
To prove a dynamical system is reversible.
A method of proving a system is reversible is illustrated in example 5 in the handbook.
Phase portrait of a reversible system.
Reversible systems have the property that if {x(t),y(t)}is a solution of the system so is {x(-t),y(-t)}. Thus the phase portrait is symmetrical about either the x-axis or the y-axis.
Stability of equilibria in a reversible system.
Theorem: If a reversible system has an equilibrium point which has a linearisation with a centre the nonlinear system must have a nonlinear centre.
Thus a reversible system can be useful in proving the existence of a nonlinear centre. The method is illustrated in the example below. Click on worked example 6 to open the relevant Maple window.
Lyapunov Functions are named after the Russian mathematician Alexander Lyapunov.(1857-1918). For a two dimensional system a Lyapunov Function has the following definition. This can be extended to three dimensions.
Definition: A function V(x,y) is a Lyapunov function for a system
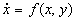
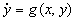
provided that along each solution of the system
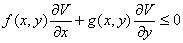
for every solution (x(t),y(t)) that is not an equilibrium point with strict inequality except for a discrete set of tís.
To verify a function is a Lyapunov function for a system.
A method of proving a function is a Lyapunov function for a system is illustrated in the example below. Click on worked example 7 to open the Maple window.
Stability of equilibria using Lyapunov functions.
How can Lyapunov funstions help you to understand the long term behaviour of a nonlinear system?
Investigation2
You are going to draw the phase portrait of a nonlinear system and the level curves of a Lyapunov function for that system. You are going to examine the two diagrams to see if you can see a connection between them. Click on Investigation 2 which opens the Maple window containing the material for this investigation.
As before if the point (p,q) is an isolated equilibrium point of the system and (p,q) is a stationary point of V(x,y) then the level curves of V(x,y) are closed curves surrounding (p,q). Since V(x,y) is a decreasing function then as t increases a non equilibrium solution of the system must move across the level curves in a direction in which V(x,y) decreases. This enables the stability of the equilibrium point to be determined and is summarised in the following theorem.
Theorem: If
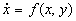
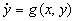
is a system of equations and V(x,y) is a Lyapunov function for the system
that has continuous first and second partial derivatives. Assume
that the only way for which![]() can
remain zero along a solution for any length of time is if the solution
is an equilibrium. Then if (p,q) is an isolated equilibrium point.
can
remain zero along a solution for any length of time is if the solution
is an equilibrium. Then if (p,q) is an isolated equilibrium point.
If the equilibrium point is also a local minimum of V(x,y) then the solution of the system must tend to (p,q) as t approaches infinity. The equilibrium point (p,q) is therefore an attractor and stable.
If the equilibrium point is also a local maximum of V(x,y) then the solution of the system must move away from (p,q) as t approaches infinity and the equilibrium point is a repeller and therefore unstable.
If the equilibrium point is also a saddle point of V(x,y) then the phase portrait of the system also resembles a saddle with the solution curves again crossing the level curves of V.
Note that this method can be used to investigate the stability of equilibrium points for both simple and nonsimple systems of equations.The following example illustratrs the method. Click on worked example 8 to open the Maple window.